 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 Derek |
 Blurred Derek |
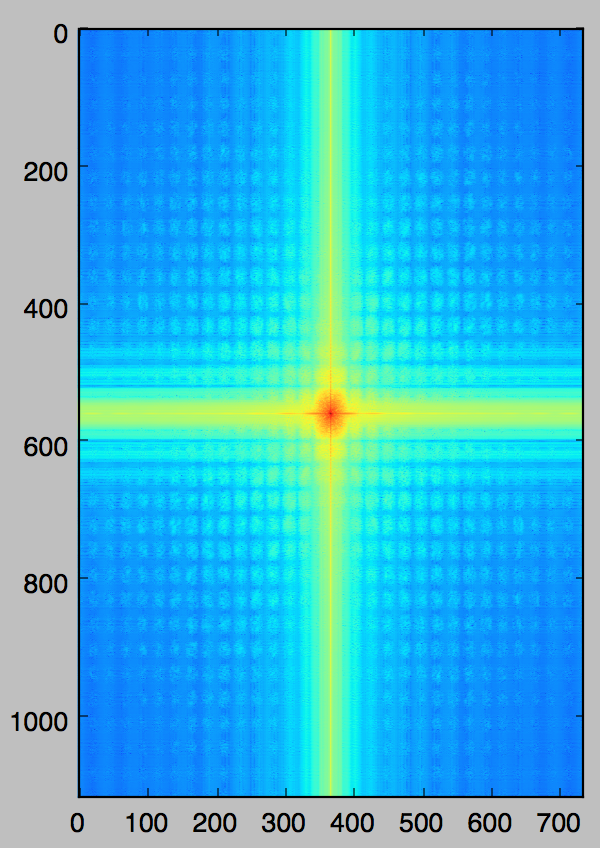 Derek's Spectrum |
 Nutmeg |
 High-pass Filtered Nutmeg |
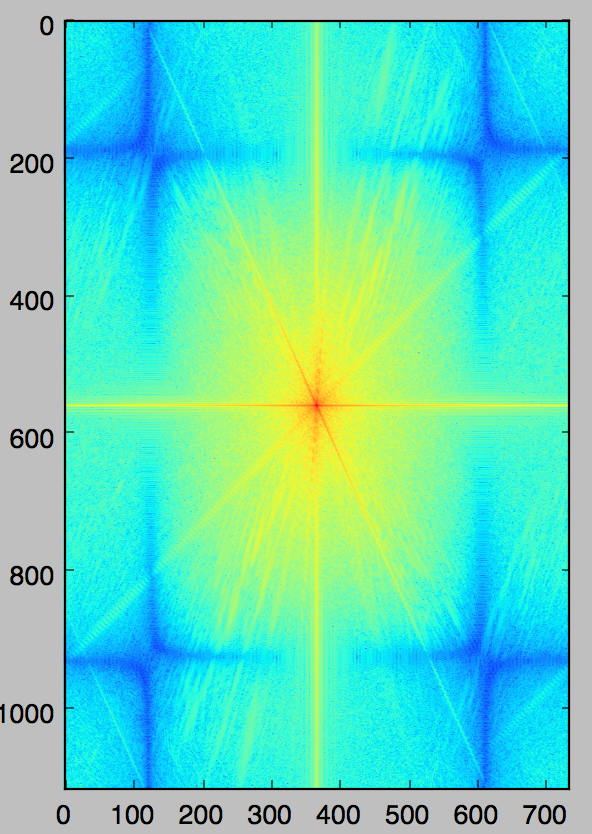 Nutmeg's Spectrum |
 Blended Image |
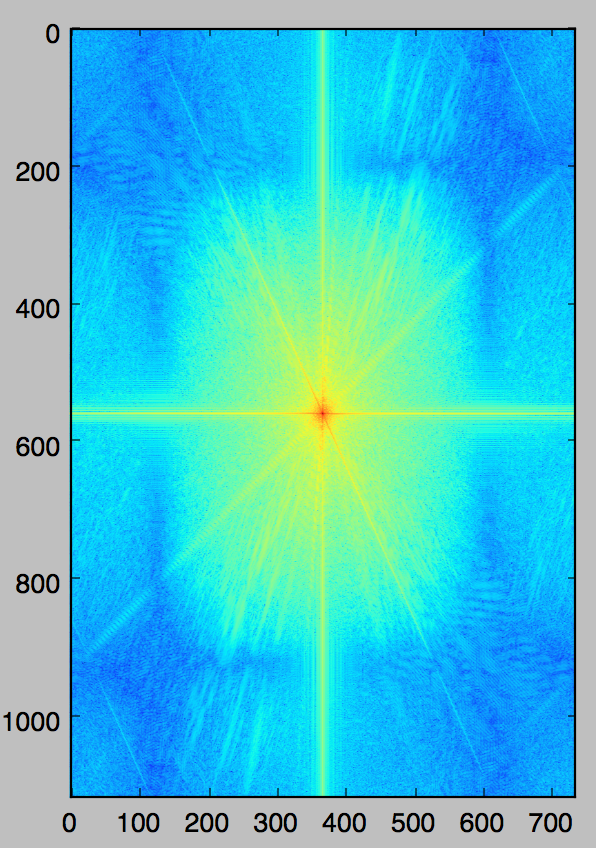 Blended Image Spectrum |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |

|

|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |

|

|

|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |