Lately, I’ve been reading through Iain M. Banks’ 5th Culture novel Excession. This book in particular gives the reader a more detailed understanding of the Culture’s Minds, the AI machines that (using a miniscule fraction of their actual abilities) plan and run their post-scarcity, anarcho-communistic society. Along the way, I stumbled upon a section describing what Minds do when they’re bored.

The Minds call it Infinite Fun Space.
The space of all possible mathematical worlds, free to explore and to play in.
It is infinitely more expressive than the boring base reality and much more varied: base reality is after all just a special case.
From time to time the Minds have to go back to it to fix some local mess, but their hearts are in Infinite Fun Space.

As described in Wikipedia

The mental capabilities of Minds are described in Excession to be vast enough to run entire universe-simulations inside their own imaginations, exploring metamathical (a fictional branch of metamathematics) scenarios, an activity addictive enough to cause some Minds to totally withdraw from caring about our own physical reality into “Infinite Fun Space”, their own, ironic and understated term for this sort of activity.

I found this to be rather apt terminology to describe my recent activities aimed at improving my mathematical intuition. A step down from simulating universes, I’ve recently been tinkering with linear algebra concepts through what I might also refer to as “mathematical daydreaming”. Yes, I know it sounds rather silly, but since the goal is develop good intuition, being able to move fluidly between ideas is key. Starting with the most basic of principles (e.g. what do the rows and columns of a matrix mean, what does a dot product do?, etc.) I’ve been slowly populating this space with various properties and theorems that I’ve derived (informally) from first principles. I try to explore the neighborhood around existing concepts, sometimes drawing connections between previously disparate groups. All the while I try to ask myself why certain concepts exist to begin with.

Sometimes, this process is guided by there being a concept that I want to understand (e.g. SVD) which I then work towards by first thinking for about the related basic concepts (such as dyads: how to do a 1-d matrix approximation using a dyad, recalling that multiplying two matrices \(A\)/\(B\) can be seen as the sum of dyads from their columns/rows). Just earlier today, I was reasoning about the optimality of the Simplex algorithm and how the properties of symmetric matrices relate to the covariance matrix (in the meantime recalling that \(x^TAx\) is equivalent to an elementwise product between the “self-dyad” \(xx^T\) and \(A\)). For additional intuition, I sometimes wrote toy programs to visualize and numerically evaluate certain illustrating examples.

\[A = \begin{bmatrix} 8 & -1 \\ 1 & 4 \end{bmatrix}\] \[v_1 = \begin{pmatrix} 0.96592583 & 0.25881905\end{pmatrix}\] \[v_2 = \begin{pmatrix} 0.25881905 & 0.96592583\end{pmatrix}\] \[\lambda_1, \lambda_2 = 7.73205081, 4.26794919\]

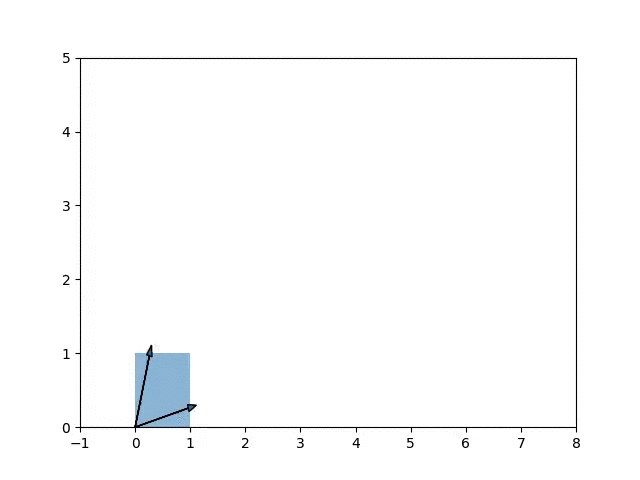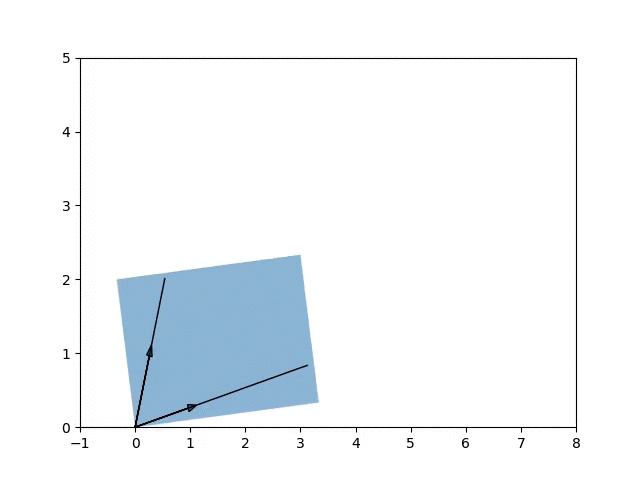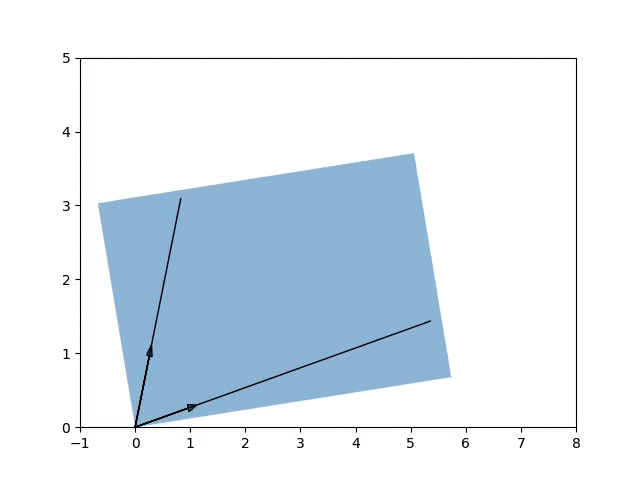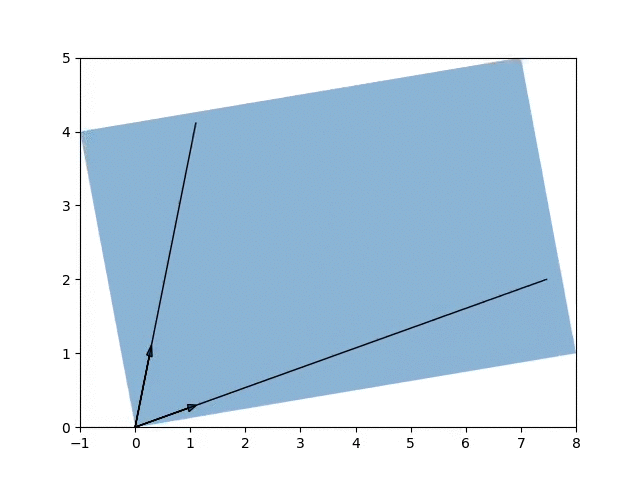
The animation shows the growth of components along the eigenvectors of \(A\) when applying the matrix A onto the unit square.

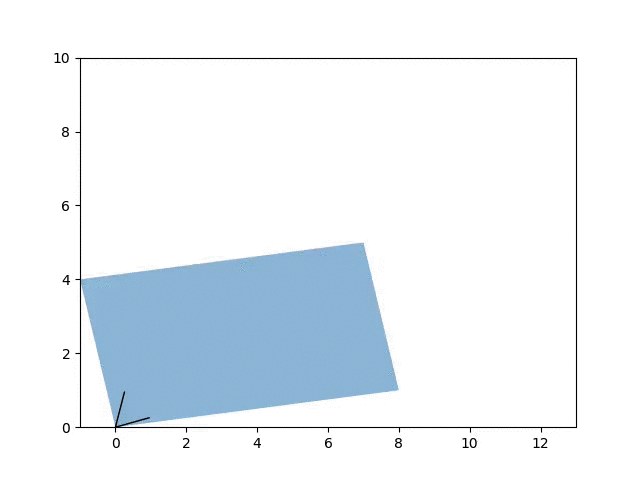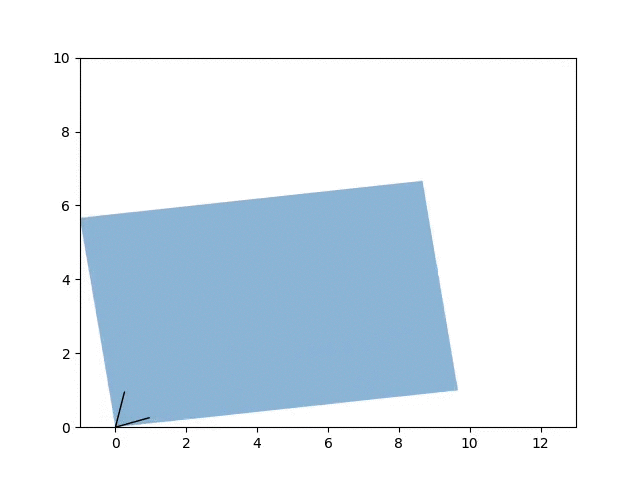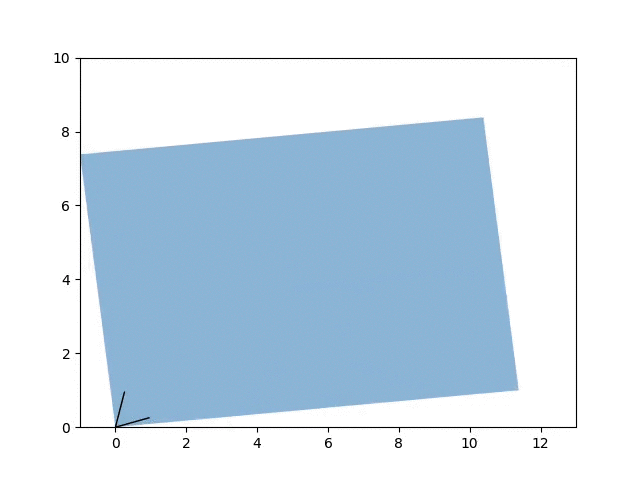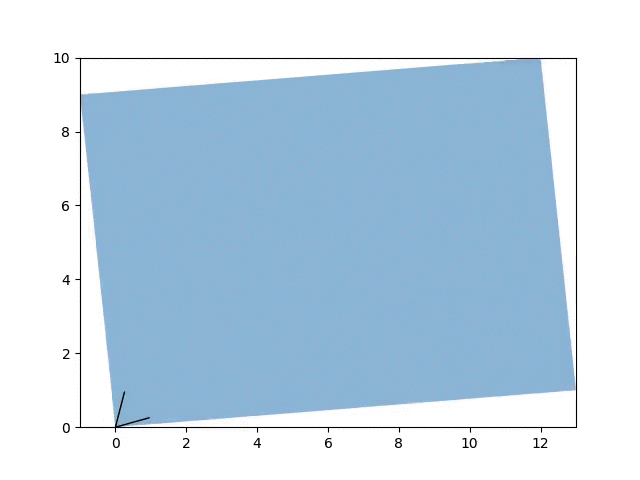
Visualizing the effect of adding between 0 and 5 to the diagonals of \(A\) on its eigenvectors. A friendly reminder that adding to the diagonal increases the eigenvalues but has no effect on the eigenvectors themselves.

Overall, this has helped a ton with retention as well as fluency. I’m far more comfortable reasoning about eigenvalues and linear transformations than I was just a few weeks ago. It’s sometimes quite slow — occasionally spending days thinking about a single concept only to find a simple uninteresting solution from an seemingly unrelated source — but I’m quite surprised how easy (and fun!) it is to get lost in thought. Similar to the drawbacks of search engines, I find I learn more by bouncing around until I can half-approximate a proof than trying to directly prove it with no context. I have yet to replicate this on other areas such as probability, statistics, and optimization but hope to do so at some point. One important thing to note is that this requires at least some familiarity with the topic. For an area with unknown unknowns (such as abstract algebra) I’m guessing that I’ll need at least a semi-formal pass at the material before I can start playing with it on my own. Eventually, I hope to achieve a better balance between working on concrete problems and this mathematical daydreaming thing. In the meantime, I’ll continue playing around in Infinite Finite and Slowly Growing Fun Space.